
张量分解-Block term decomposition (BTD)
去年差不多这个时候,我在本人的博客上发表了三个关于张量分解的博客,从百度统计来看,很多人阅读了这三篇博文。今天,我再介绍一种张量分解-block term decomposition (BTD),下面将分几个部分对BTD进行介绍。
从CP分解到BTD
在CP分解中我们将一个张量分解为 K个Rank1的成员张量的形式,写成公式即为: \begin{equation} \mathcal{T}=\sum \limits_{r = 1}^{K}a_r\circ b_r \circ c_r=\sum \limits_{r = 1}^{K} (a_rb_r^T)\circ c_r \end{equation} 显然$a_rb_r^T$是一个Rank-1的矩阵,即一个低秩矩阵。而低秩往往是一些局部的特征,比如说人的一些眉毛一般都是低秩的。而在一些应用中,我们想得到一些不同秩的特征,或者是不同尺度的特征,比如说对于人脸,我想得到鼻子,眉毛,嘴巴,脸型等特征,这个时候CP分解就无法直观地做到了。
基于CP分解,我们想,如果$a_rb_r^T$,它不是一个秩为1️的矩阵,而是一个秩为K的矩阵,那么显然$a_r$和$b_r$就不是一个向量了,而是一个秩为$L_r$的矩阵。于是就得到了BTD模型的一种形式即 \begin{equation} \mathcal{T}=\sum \limits_{r = 1}^{K}A_rB_r^T\circ c_r \end{equation}
可以将这个模型进一步进行推导即可得到BTD的通俗形式。
BTD分解概览
2008年Lieven De Lathauwer 等人提出了一种Block term decomposition(BTD),这种张量分解在一些论文中也被称为Block component decomposition (BCD)。我本人认为叫BCD 更合理一些,因为这种张量分解将一个N阶张量分解为R个成员张量的形式,BCD更符合。如下图就是一个$Rank-(L_r, M_r, N_r)$的分解,每一个成员张量是一个$Rank-(L_r, M_r, N_r)$的Tucker分解。
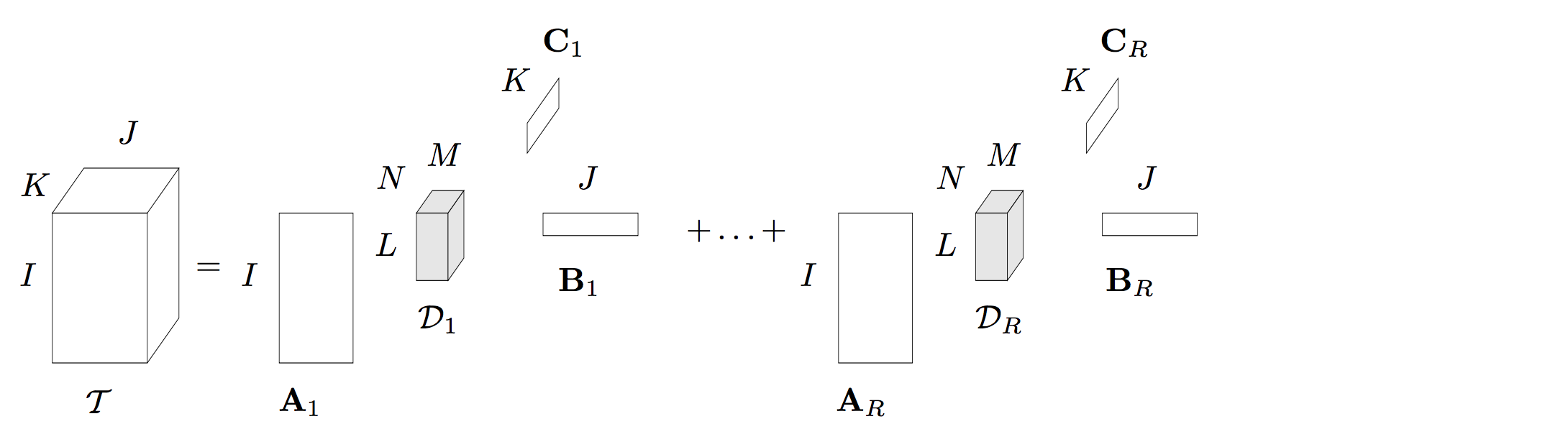
采用数学表达式可以写为:
\begin{equation} \mathcal{T}=\sum \limits_{r = 1}^{R} \mathcal{D_r}\times_{1} A_r \times_{2} B_r\times_{3}C_r\label{eq:tucker} \end{equation}
其中 $\mathcal{D_r}$是一个$Rank-(L_r, M_r, N_r)$的张量,$A_r\in R^{I\times L}$是一个秩为I的矩阵。显然BTD可以看出该分解可以看作是我们之前介绍的Tucker分解和CP分解的结合形式。当$R=1$的时候,显然成员张量只有一个,此时这个分解就是个$Rank-(L, M, N)$的Tucker分解。而当每一个成员张量是一个$Rank -1$分解的时候,该分解退化为一个CP分解 (CP分解是将一个张量分解为R个 秩为1的张量分解形式)。这也说明了,BTD分解具有很强的泛化能力。论文 http://epubs.siam.org/doi/pdf/10.1137/070690730 同时对它的唯一性进行了证明,从证明来看,该算法的唯一性的条件要比Tucker分解和CP分解的唯一性要弱。
BTD分解的求解
BTD分解现在的求解算法有很多,比如说非线性最小二乘法,交替最小二乘算法(ALS),张量对角算法等,其中交替最小二乘算法形式最为简单,下面我们以一个三阶张量$\mathcal{T} \in ^{I\times J \times K}$的张量为例,这种求解算法进行介绍。
定义$A=[A_1,\cdots,A_R]$,$B=[B_1,\cdots,B_R]$ $C=[C_1,\cdots,C_R]$将BTD写为矩阵的形式,可以得到如下三个表达式:
\begin{equation} T_{JK\times I}=(B\otimes C). Blockdiag(\mathcal{D}_{1_{MN\times L}}, \cdots,\mathcal{D}_{R_{MN\times L}})A^{T} \end{equation}
\begin{equation} T_{KI\times J}=(C\otimes A). Blockdiag(\mathcal{D}_{1_{NL\times M}}, \cdots,\mathcal{D}_{R_{NL\times M}})B^{T} \end{equation}
\begin{equation} T_{IJ\times K}=(A\otimes B). Blockdiag(\mathcal{D}_{1_{LM\times N}}, \cdots,\mathcal{D}_{R_{LM\times N}})C^{T} \end{equation}
当更新某一个因子矩阵或者张量的时候,固定其它元素即可进行求解。如当求解$A$时,固定$\mathcal{D_r}$和$B$以及$C$,设置$M=(B\otimes C). Blockdiag(\mathcal{D}_{1_{MN\times L}}, \cdots,\mathcal{D}_{R_{MN\times L}})$因此,我们可以得到$A$的更新规则为
\begin{equation} A=M^{\dagger}.T_{JK\times I} \end{equation}
同理可以得到其它矩阵或者张量的更新规则。因此采用ALS算法求解BTD的步骤如下:

算法中的QR分解是为了防止算法出现数值计算错误。
特殊BTD分解
在前面我们已经介绍了BTD分解的两种特殊形式:Tucker分解和CP分解。下面我们再介绍两种特殊的张量分解。
Rank-(Lr,Lr,1)分解
当每一个成员张量退化为$L_r\times L_r$的矩阵时,可以得到$Rank-(L_r,L_r,1)$分解即:
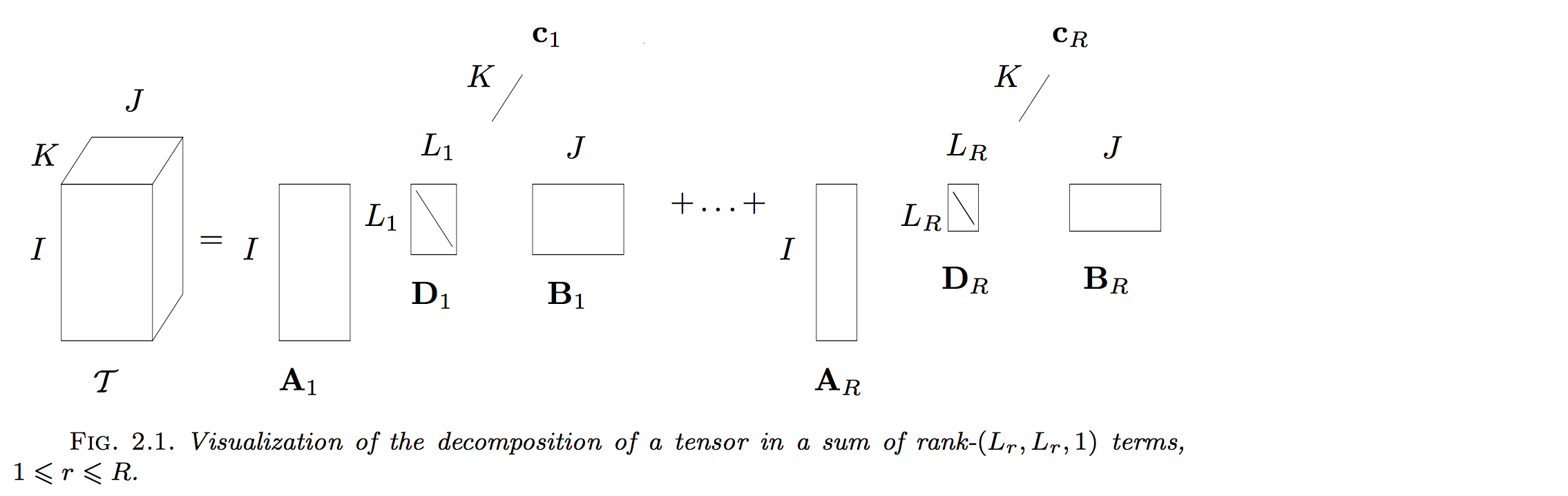
相应的求解算法和BTD算法类似,只是没有了最后一步的求解core tensor部分。

Rank-(L,L,1)分解
当$Rank-(L_r,L_r,1)$的每一个$L_r$取值为一致即$L$时候即可得到$Rank-(L,L,1)$分解即:
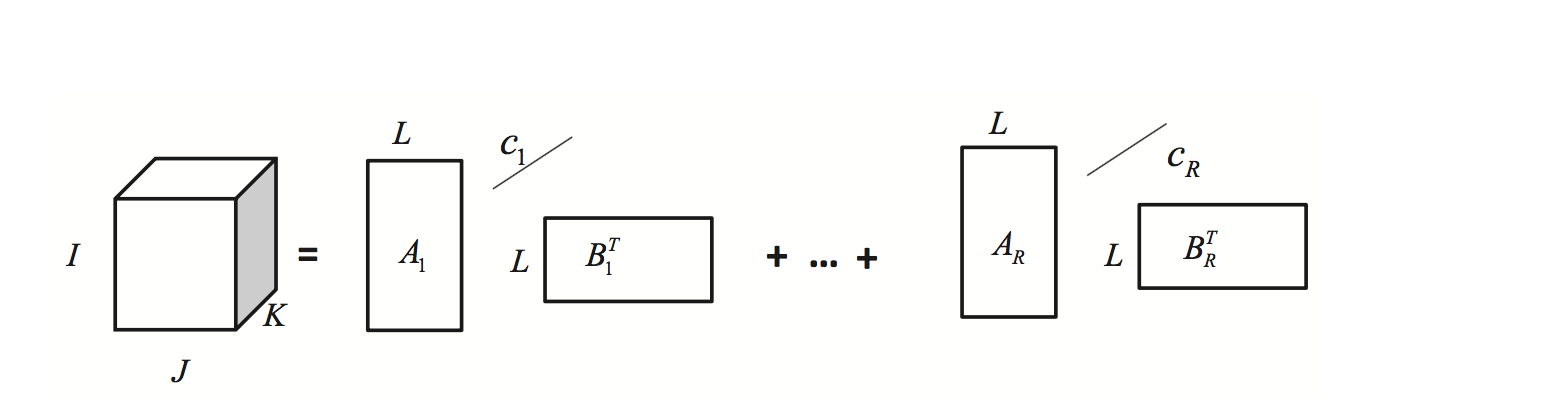
BTD分解的应用
BTD分解的现阶段的主要应用在盲源分离上,尤其是它的蜕化形式$Rank-(L,L,1)$形式。 在$Rank-(L,L,1)$中$c_r$可以看作是一个信号,$A_r\times B_r$可以看作是混合矩阵的低秩表达形式。本人也基于此分解在IEEE TGRS上发表了一篇题为“Matrix-Vector Nonnegative Tensor Factorization for Blind Unmixing of Hyperspectral Imagery”的文章,具体可以看 http://www.cs.zju.edu.cn/people/qianyt/paper/Matrix-Vector%20Nonnegative%20Tensor%20Factorization%20for%20Blind%20Unmixing%20of%20Hyperspectral%20Imagery.pdf。
另外,BTD分解现在也开始应用在深度学习中(事实上张量分解在深度学习中的应用最近被广泛地被研究,因为张量分解可以有效地减少深度学习中参数的个数,具体可以Google Tensor deep learning )。新加坡国立大学颜水成教授2017年发表了一篇题为Sharing Residual Units Through Collective Tensor Factorization in Deep Neural Networks 的文章,这篇文章中,用BTD分解来代替残差网路中的卷积单元(没有仔细读,等仔细读之后再详细写)
