张量分解-Tucker分解
Tucker分解
Tucker的1966年文章中第一次提到了Tucker分解。一个三阶张量的Tucker分解的图示如下图所示。
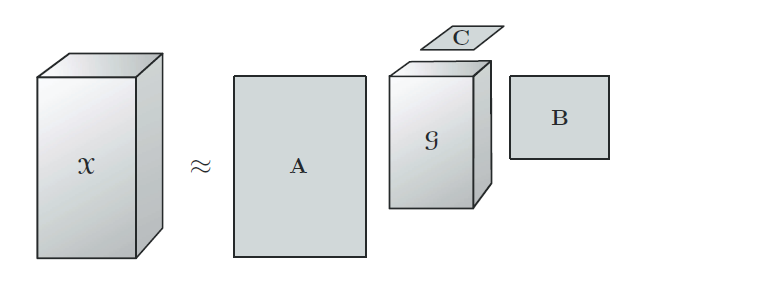
对于一个三阶张量$\mathcal{X}\in \mathbb{R}^{I\times J \times K}$, 由Tucker分解可以得到$A\in \mathbb{R}^{I\times P}$,$B\in \mathbb{R}^{J\times Q}$,$C\in \mathbb {R}^{K\times R}$三个因子矩阵和一个核张量 $\mathcal{G}\in \mathbb{R}^{P\times Q\times R}$,每个mode上的因子矩阵称为张量在每个mode上的基矩阵或者是主成分,因此Tucker 分解又称为高阶PCA, 高阶SVD等。从图中可以看出，CP分解是Tucker分解的一种特殊形式：如果核张量的各个维数相同并且是对角的,则Tucker分解就退化成了CP分解。
在三阶张量形式中,有
\begin{equation}
\mathcal{X}=\mathcal{G}\times_{1} A \times_{2} B\times_{3}C=\sum \limits_{p = 1}^{{P}}\sum \limits_{q = 1}^{Q}\sum \limits_{r = 1}^{R}g_{pqr}a_{p}\circ b_{q} \circ c_{r}=\left[\kern-0.15em\left[ {\mathcal{G} ; A,B,C}\right]\kern-0.15em\right]\label{eq:tucker}
\end{equation}
将上面的公式写成矩阵的形式即:
\begin{equation}
\begin{split}
&X_{1}=AG_{(1)}(C\otimes B)^{T}
&X_{2}=BG_{(2)}(C\otimes A)^{T}
&X_{3}=CG_{(3)}(B\otimes A)^{T}
\end{split}\label{eq:tuckerMatrix}
\end{equation}
对于三阶张量固定一个因子矩阵为单位阵，就得到Tucker分解一个重要的特例：Tucker2。例如固定$C=I$，则退化为:
\begin{equation}
\mathcal{X}=\mathcal{G}\times_{1} A \times_{2} B=\left[\kern-0.15em\left[ {\mathcal{G} ; A,B,I}
\right]\kern-0.15em\right]\label{eq:tucker2}
\end{equation}
进一步，如果固定两个因子矩阵，就得到了Tucker1例如固定$C=I$,$B=I$，则Tucker 分解就退化成了普通的PCA
\begin{equation}
\mathcal{X}=\mathcal{G}\times_{1} A =\left[\kern-0.15em\left[ {\mathcal{G} ; A,I,I}
\right]\kern-0.15em\right]\label{eq:tucker1}
\end{equation}
把上面的公式推广到$N$阶的模型即可得到:
\begin{equation}
\mathcal{X}=\mathcal{G}\times_{1} A^{(1)} \times_{2} A^{(2)}\cdots \times_{(N)}A^{(N)}=\left[\kern-0.15em\left[ {\mathcal{G} ; A^{(1)} ,A^{(2)} ,\cdots,A^{(N)} }
\right]\kern-0.15em\right]\label{eq:tuckerNmode}
\end{equation}
写成矩阵形式即:
\begin{equation}
X_{(n)}=A^{(n)}G_{(n)}(A^{(N)}\otimes \cdots \otimes A^{(n+1)}\otimes A^{(n-1)}\cdots \otimes A^{(1)} )^{T}
\label{eq:tuckerMatrixNmode}
\end{equation}
n-秩与低秩近似
$n$-秩又称为多线性秩。一个N阶张量$\mathcal{X}$的n-mode秩定义为：
\begin{equation}
rank_{n}(\mathcal{X})=rank(X_{(n)})
\end{equation}
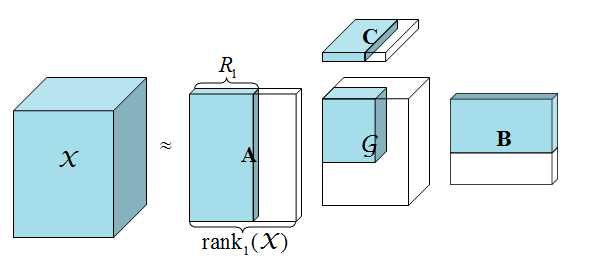
令$rank_{n}(\mathcal{X})=R_{n},n=1,\cdots ,N$则$\mathcal{X}$叫做秩$(R_1,R_2,\cdots,R_n)$的张量。$R_n$可以看作是张量$\mathcal{X}$在各个mode上fiber所构成的空间的维度。如果${\text{ran}}{{\text{k}}_n}(\mathcal{X}) = {R_n},n = 1, \cdots ,N$，则很容易得到$\mathcal{X}$的一个精确秩-$\left({{R_1},{R_2}, \cdots ,{R_N}} \right)$Tucker分解；然而如果至少有一个 $n$ 使得 $ {\text{ran}}{{\text{k}}_n}(\mathcal{X}) > {R_n}$，则通过Tucker分解得到的就是$\mathcal{X}$的一个秩- $\left({{R_1},{R_2}, \cdots ,{R_N}} \right)$近似。下图展示了一个三阶张量的低秩近似,这个在图像处理中有可以认为是干净的图像。
Tucker分解的求解
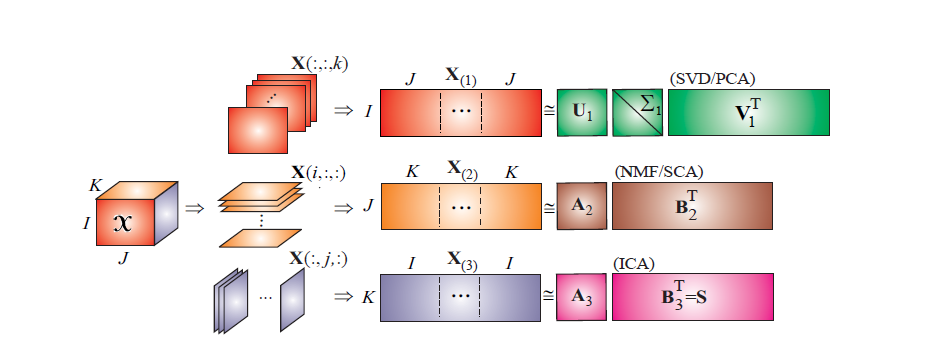
对于固定的$n$-秩，Tucker分解的唯一性不能保证，一般加上一些约束，如分解得到的因子单位正交约束等。比如HOSVD(High Order SVD)求解算法,它通过张量的每一个mode上做SVD分解对各个mode上的因子矩阵进行求解,最后计算张量在各个mode上的投影之后的张量作为核张量。它的算法过程如下图所示。
虽然利用SVD对每个mode做一次Tucker1分解,但是HOSVD 不能保证得到一个较好的近似，但HOSVD的结果可以作为一个其他迭代算法（如HOOI）的很好的初始化。(\textit{High-order orthogonal iteration})HOOI算法,将张量分解看作是一个优化的过程,不断迭代得到分解结果。假设有一个$N$ 阶张量$\mathcal{X} \in \mathbb{R}^{I_1 \times I_2 \times \cdots \times I_N }$,那么对$\mathcal{X}$进行分解就是对下面的问题进行求解:
\begin{equation}
\begin{gathered}
{\text{ }}\left| {\mathcal{X} - \left[\kern-0.15em\left[ {\mathcal{G};{{\mathbf{A}}^{(1)}}, \cdots ,{{\mathbf{A}}^{(N)}}}
\right]\kern-0.15em\right]} \right| \hfill \
= \left| {{\text{vec}}(\mathcal{X}) - \left( {{{\mathbf{A}}^{(N)}} \otimes \cdots \otimes {{\mathbf{A}}^{(1)}}} \right){\text{vec}}(\mathcal{G})} \right| \hfill \
\end{gathered} \label{eq:tuckerObj}
\end{equation}
将上述的目标函数进一步化简得到:
\begin{equation}
\begin{gathered}
{\text{ }}{\left\| {\mathcal{X} - \left[\kern-0.15em\left[ {\mathcal{G};{{\mathbf{A}}^{(1)}}, \cdots ,{{\mathbf{A}}^{(N)}}}
\right]\kern-0.15em\right]} \right\|^2} \hfill \
= {\left\| \mathcal{X} \right\|^2} - 2\left\langle {\mathcal{X},\left[\kern-0.15em\left[ {\mathcal{G};{{\mathbf{A}}^{(1)}}, \cdots ,{{\mathbf{A}}^{(N)}}}
\right]\kern-0.15em\right]} \right\rangle + {\left| {\left[\kern-0.15em\left[ {\mathcal{G};{{\mathbf{A}}^{(1)}}, \cdots ,{{\mathbf{A}}^{(N)}}}
\right]\kern-0.15em\right]} \right|^2} \hfill \
= {\left\| \mathcal{X} \right\|^2} - 2\left\langle {\mathcal{X}{ \times_1}{{\mathbf{A}}^{(1){\text{T}}}} \cdots { \times_N}{{\mathbf{A}}^{(N){\text{T}}}},\mathcal{G}} \right\rangle + {\left\| \mathcal{G} \right\|^2} \hfill \
= {\left\| \mathcal{X} \right|^2} - 2\left\langle {\mathcal{G},\mathcal{G}} \right\rangle + {\left\| \mathcal{G} \right\|^2} \hfill \
\end{gathered} \label{eq:tuckerTemp}
\end{equation}
而$\mathcal{G}$满足
\begin{equation}
\mathcal{G} = \mathcal{X}{\times_1}{{\mathbf{A}}^{(1){\text{T}}}} \cdots { \times_N}{{\mathbf{A}}^{(N){\text{T}}}}\label{eq:tuckerCoreTensor}
\end{equation}
从而可与可以得到:
\begin{equation}
= {\left\| \mathcal{X} \right\|^2} - {\left\| {\mathcal{X}{ \times_1}{{\mathbf{A}}^{(1){\text{T}}}} \cdots { \times_N}{{\mathbf{A}}^{(N){\text{T}}}}} \right\|^2}\label{eq:tuckerMin}
\end{equation}
由于$\|\mathcal{X}\|$是一个常数,最小化上面的式子相当于最大化:
\begin{equation}
\begin{split}
&\max \left\| {\mathcal{X}{\times _1}{{\mathbf{A}}^{(1){\text{T}}}} \cdots {\times_N}{{\mathbf{A}}^{(N){\text{T}}}}} \right\|
subject \quad to \quad A^{(n)\in \mathbb{I_n\times R_n}} \quad and \quad columnwise \quad orthogonal
\end{split} \label{eq:tuckerMax}
\end{equation}
写成矩阵形式即:
\begin{equation}
\begin{gathered}
\max \left\| {{{\mathbf{A}}^{(n){\text{T}}}}{\mathbf{W}}} \right\| \hfill \
{\text{s}}{\text{.t}}{\text{. }}{\mathbf{W}} = {{\mathbf{X}}_{(n)}}\left( {{{\mathbf{A}}^{(N)}} \otimes \cdots \otimes {{\mathbf{A}}^{(n + 1)}} \otimes {{\mathbf{A}}^{(n - 1)}} \cdots \otimes {{\mathbf{A}}^{(1)}}} \right) \hfill
\end{gathered}
\end{equation}
这个问题可以通过令${{\mathbf{A}}^{(n)}}$ 为 $W$ 的前 ${R_n}$ 个左奇异值向量来进行求解。HOOI算法的过程如下图所示。
约束Tucker的分解
除了可以在Tucker分解的各个因子矩阵上加上正交约束以外,还可以加一些其它约束,比如稀疏约束,平滑约束,非负约束等。另外在一些应用的场景中不同的mode的物理意义不同，可以加上不同的约束。在下图中在三个不同的mode上分别加上了正交约束,非负约束以及统计独立性约束等。
Tucker的分解的应用
前面我们说Tucker分解可以看作是一个PCA的多线性版本,因此可以用于数据降维,特征提取,张量子空间学习等。比如说一个低秩的张量近似可以做一些去噪的操作等。Tucker分解同时在高光谱图像中也有所应用，如用低秩Tucker分解做高光谱图像的去噪,用张量子空间做高光谱图像的特征选择,用Tucker分解做数据的压缩等。下面以高光谱图像去噪为例作相关的介绍。
http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=6909773中对高光谱图像去噪的流程如下图所示，
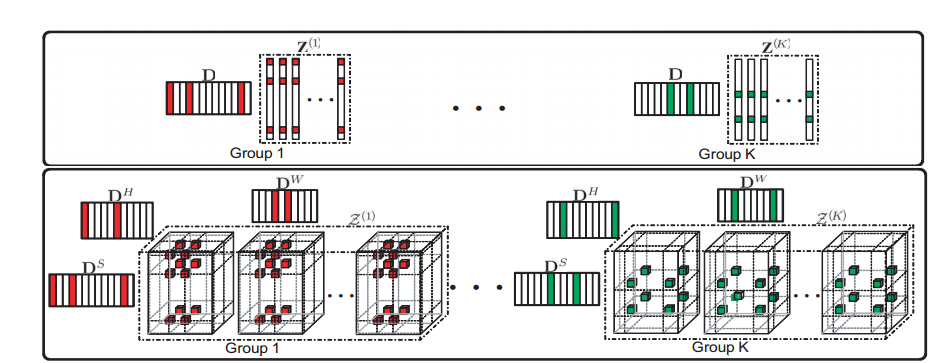它首先对高光谱图像进行分块，然后对分的快进行聚类，得到一些group，最后对各个group里面的数据进行低秩Tucker分解。处理之前的噪声图像和处理之后的图像的对比如下图所示,可以发现Tucker分解可以对高光谱数据做有效的去噪处理。
