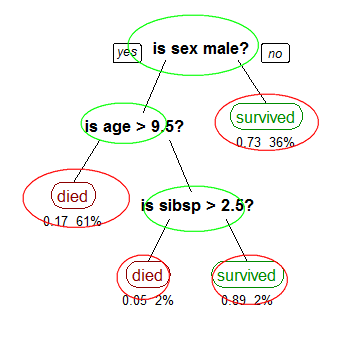《机器学习实战》--决策树算法 2014.03.19

一、决策树算法的概念

决策树其实就是我们数据结构中的一棵树，它很普遍，比如说我们经常写的分支语句，if  then—else  if  else 其实就是一颗决策树。。它是一种监督性的学习方法，它假设所有的特征都有其确定有限的域，对于每一个域其都有一个目标特征称为分类。它的每一个非叶子节点表示一个输入条件，而叶子节点表示结果。

 

如图所示，就是一个决策树，用红线标注的都是一个个分类，而用绿色标注的是一个个决策的输入条件。

根据这个条件我们可以得出一些规则出来比如说：

IF SEX!=MALE THEN SURVIED;

IF  SEX==MALE AND AGE>9.5 THEN DIED；

这些规则可以用来对其它的数据进行分类。

二、决策树的构造

首先决策树的构造第一个要解决的问题就是当前哪个特征在划分数据分类中起到决定性的作用，为了确定决定性的特征，我们需要对特征进行评估，以便对数据进行划分。在评估上面我们采用信息增益方式进行计算。首先类别C是变量，它可能的取值是C₁，C₂，……，C_n，而每一个类别出现的概率是P(C₁)，P(C₂)，……，P(C_n)，因此n就是类别的总数\[(H(C) = - \sum\limits_{i = 1}^n {p({C_i})*{{\log }_2}p({C_i})} {\rm{ }}\]而对于特征X，它可能的取值有n多种（x₁，x₂，……，x_n），其条件熵为 那么对于特征X其信息增益为哪个特征的信息增益大，我们就选择哪个作为数据划分的决定性因子。故而有以下代码：

1.计算给定数据集的熵

def calcShannonEnt(dataSet):
以下7行代码用来计算数据中每一种类别出现的次数
    numEntries = len(dataSet);
    labelCounts = {}
    for data in dataSet:
        currentLabel = data[-1];
        if(currentLabel not in labelCounts.keys()):
            labelCounts[currentLabel] = 0;
        labelCounts[currentLabel] += 1;
    shannonEnt = 0.0;
以下用来计算每一种类别的熵
    for key in labelCounts.keys():
        prob = float(labelCounts[key]) / numEntries;
        shannonEnt = shannonEnt - prob * log(prob, 2);
    return shannonEnt;

2.按照给定特征划分数据集

def splitDataSet(dataSet, axis, value):
    retDataSet = [];
    for featVec in dataSet:
        if featVec[axis] == value:
进行数据切片，根据给定的特征进行数据集的划分，注意这里的extend和append extend表示在原有的数组中进行扩展，而append表示在在原有的#数据中进行追加 比如说[1,2,3].extend([4,5,6])那么结果为[1,2,3,4,5,6],而[1,2,3].append[4,5,6]结果为[1,2,3,[4,5,6]]
            reducedFeatVec = featVec[:axis];
            reducedFeatVec.extend(featVec[axis + 1:]);
            retDataSet.append(reducedFeatVec);
    return retDataSet;

3.选择最好的数据集划分方式：

def chooseBestFeatureToSplit(dataSet):
    numFeatures = len(dataSet[0]) - 1;#计算特征个数
    baseEntropy = calcShannonEnt(dataSet);#计算原始熵
    bestInfoGain = 0.0;bestFeature = -1;
根据每一个特征进行数据的划分，最终找出信息增益最大的特征返回
    for i in range(numFeatures):
        featList = [example[i] for example in dataSet];
        uniqueVals = set(featList);
        newEntropy = 0.0;
        for value in uniqueVals:
            subDataSet = splitDataSet(dataSet, i, value);
            prob = len(subDataSet) / float(len(dataSet));
            newEntropy += prob * calcShannonEnt(subDataSet);
        infoGain = baseEntropy - newEntropy;
        if(infoGain > bestInfoGain):
            bestInfoGain = infoGain;
            bestFeature = i;
    return bestFeature;

4.创建决策树

def createTree(dataSet, labels):
    classList = [example[-1] for example in dataSet]
    if classList.count(classList[0]) == len(classList): 
        return classList[0]  # 类别相同则停止划分
    if len(dataSet[0]) == 1:  # 遍历完所有特征之后返回出现次数最多的
        return majorityCnt(classList)
    bestFeat = chooseBestFeatureToSplit(dataSet)
    bestFeatLabel = labels[bestFeat]
    myTree = {bestFeatLabel:{}}
    del(labels[bestFeat])#得到列表包含的所有属性值
    featValues = [example[bestFeat] for example in dataSet]
    uniqueVals = set(featValues)
    for value in uniqueVals:
        subLabels = labels[:]  # copy all of labels, so trees don't mess up existing labels
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels)
    return myTree

如果我们输入以下的数据集和标签

dataSet = [[1, 1, ‘yes’], [1, 1, ‘yes’], [1, 0, ‘no’], [0, 1, ‘no’], [0, 1, ‘no’] ]; labels = [‘no surfacing’, ‘flippers’];

那么可以得到结果为{‘no surfacing’: {0: ‘no’, 1: {‘flippers’: {0: ‘no’, 1: ‘yes’}}}}其对应的决策树为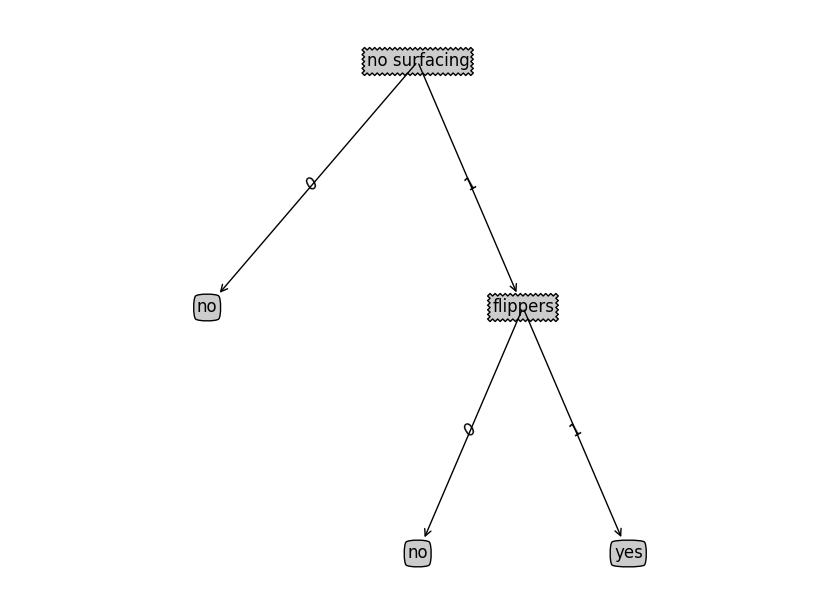

具体的可视化的代码可以见《机器学习实战》一书。

那么对于任意输入的测试数据进行分类的代码如下：

def classify(inputTree,featLabels,testVec):
    firstStr = inputTree.keys()[0]
    secondDict = inputTree[firstStr]
    featIndex = featLabels.index(firstStr)
    key = testVec[featIndex]
    valueOfFeat = secondDict[key]
    if isinstance(valueOfFeat, dict): 
        classLabel = classify(valueOfFeat, featLabels, testVec)
    else: classLabel = valueOfFeat
    return classLabel

三、决策树的优点、缺点和适用范围

优点：计算复杂度不高，而且简单易于理解

缺点：可能会产生过度匹配问题？？？

适用数据类型：数值型和标称型

• ← Prev
• Next →