非负矩阵分解
在这篇博文里面，我将对我所了解的非负矩阵分解进行介绍。主要对非负矩阵分解的概念以及它相关的应用进行介绍。
奇异值分解
要对非负矩阵分解进行介绍，首先我们必须先了解一下奇异值分解(singular value decomposition),简称为SVD。在SVD中我们对于任异一个$m \times n$的矩阵M，它的SVD分解的形式为： \[M = U\Sigma {V^T}\]
其中$U$和$V$是两个单位正交矩阵，分别称作矩阵$M$的左右奇异向量，矩阵$\Sigma$ 为一个对角矩阵，它的每一个元素称为矩阵$M$的奇异值，对应为谱分解(https://en.wikipedia.org/wiki/Eigendecomposition_of_a_matrix)中特征值的平方。我们知道谱分解要求矩阵必须是方阵，而且谱分解不唯一。和谱分解不同的是，任何一个矩阵都有它的奇异值分解而且它的奇异值分解是唯一的。
奇异值分解与PCA
在奇异值分解中如果我们取$\Sigma$的前K个最大值作为矩阵$M$的近似，即 $M =\sum\nolimits_{i = 1}^k { {u_i} {\sigma_i} } {v_i}^T$,这样我们就得到了矩阵$M$的低秩近似。因为新的矩阵$M$d的秩为$K$它小于原来的矩阵的秩。这种低秩近似可以用于数据降维。比如说在Principal component analysis (PCA) 分解中我们对协方差矩阵进行低秩近似以对原始的数据进行降维。这是因为在PCA为了减少数据集的维数，同时保持数据集中的对方差贡献最大的特征。我们通过对协方差矩阵进行分解保留低阶主成分，忽略高阶主成分做到。这样低阶成分往往能够保留住数据的最重要方面。它数学定义为：我们通过一个正交化线性变换，把数据变换到一个新的坐标系统中，使得这一数据的任何投影的第一大方差在第一个坐标（称为第一主成分）上，第二大方差在第二个坐标（第二主成分）上，依次类推，这个刚好和奇异值分解反应的性质一样。
奇异值分解与Latent semantic indexing (LSI)
传统向量空间模型使用精确的词匹配，即精确匹配用户输入的词与向量空间中存在的词。由于一词多义(polysemy)和一义多词(synonymy)的存在，使得该模型无法提供给用户语义层面的检索。比如用户搜索”automobile”，即汽车，传统向量空间模型仅仅会返回包含”automobile”单词的页面，而实际上包含”car”单词的页面也可能是用户所需要的。
潜在语义分析(LSI)的目的，就是要找出词(terms)在文档和查询中真正的含义，也就是潜在语义，从而解决上节所描述的问题。具体说来就是对一个大型的文档集合使用一个合理的维度建模，并将词和文档都表示到该空间，比如有2000个文档，包含7000个索引词，LSI使用一个维度为100的向量空间将文档和词表示到该空间，进而在该空间进行信息检索。而将文档表示到此空间的过程就是SVD奇异值分解和降维的过程。我们对一个Word-Document矩阵$M$进行SVD分解得到
\[M \approx {\rm{ }}{U^{\left( k \right)}}{\Sigma ^{\left( k \right)}}{V^{\left( k \right)}}^T]\]
，其中$U$我们称为潜在语义或者是topic。这样我们在计算两个文档$M_i$和$M_j$的相似度的时候我们可以把两个文档在矩阵$U$上作投影然后再计算相似度，即
\[\left. {\left\langle {{M_i}^TU,{M_j}^TU} \right.} \right\rangle \]
但是LSI中的topic有以下两个缺点
- “主题”是单位正交的
考虑主题“政治”和“金融”，我们很难说这两个主题正交(无关)
- 主题中存在负的数值
主题中存在负数表示某一个单词不属于某一个topic，这个在一些具体的应用中会有所影响，具体我也没有想好为什么会有所影响….但是在一个文档中这样描述
But then when we compute similarly, two documents are
judged to be more similar based on a topic that they are both decidedly not about.This is another counter intuitive and undesirable property
在一些实际的问题中我们往往要求所获得”topic”是非负的，比如说在高光谱图像中每一个pixel的signature要是非负的，因为负的数值在高光谱图像中是没有意义的。因此我们就得到了下面要讲的非负矩阵分解(NMF)。
非负矩阵分解##
在非负矩阵分解中我们对一个矩阵$M$进行非负近似即：
\[Y \approx AW \]
其中矩阵$A$和矩阵$W$分别为$m \times k$和$k \times n$的非负矩阵。一个简单的图示如下：
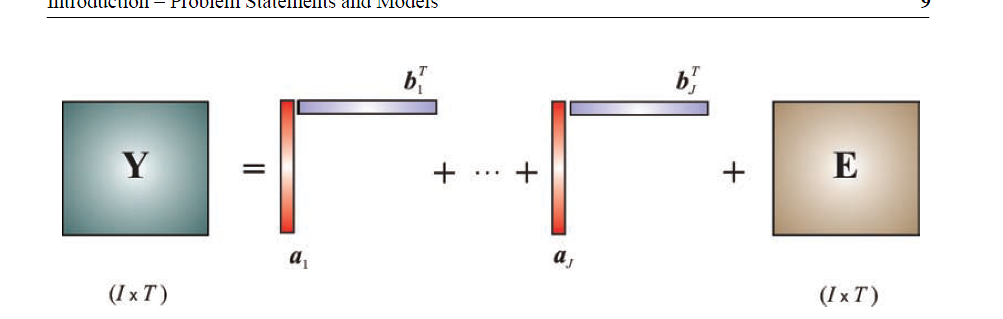
在这个图中我们把一个矩阵$Y$表示为$k$个非负的向量$a$和$k$个非负向量$b$乘积的形式。其中矩阵$E$在实际应用中表示噪声。 和SVD不同的是NMF是不唯一的，因为我们显然可以找到一个对角矩阵$D$使得$M \approx AD{D^{ - 1}}W$ 如果我们取$\mathop A\limits^~ = AD$，$\mathop M\limits^~ = {D^{ - 1}}W$，我们可以得到矩阵M的另外一个非负近似为： \[M \approx \mathop A\limits^~ \mathop W\limits^~ \]
所以我们一般会对矩阵$A$和矩阵$W$作一些约束,比如说稀疏，或者sum-to-one等等。非负矩阵分解在一些领域也有很多的应用，比如说在高光谱图像解混(Hyperspectral Unmixing)，文本的聚类等。
##非负矩阵的求解##
当我们不知道矩阵的rank r的时候，显然对于NMF，它是一个NP-hard 问题，因为我们只能对矩阵的rank进行不断的遍历求解。如果我们知道rank r我们可以通过EM的方法对目标函数进行求解。它的主要idea是，我们先对矩阵$A$和$W$进行随机猜一个数值，然后进行不断的迭代，求解直到收敛。一般在非负矩阵求解中有两种方法一个是乘法更新方法，另外一种是ALS方法。下面我们对这两种方法进行介绍。
###乘法更新求解NMF###
在乘法更新中目标函数的表达式为
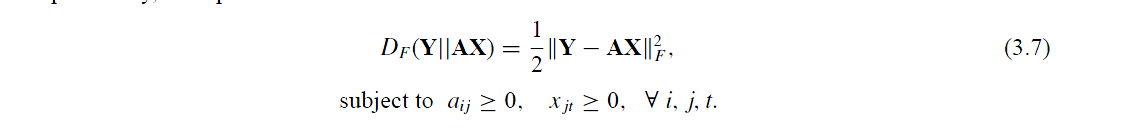然后我们对这个目标函数表达式求解KKT条件得到如下：
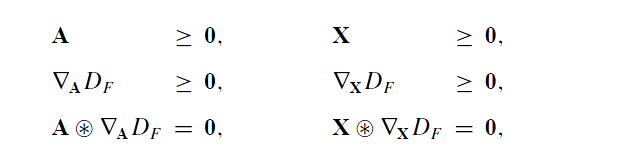其中梯度的表达式为：
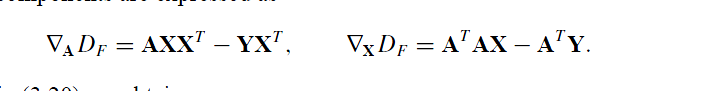结合上述的两组式子我们得到：
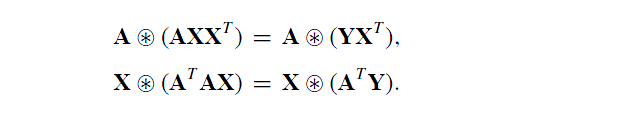即更新的规则为:
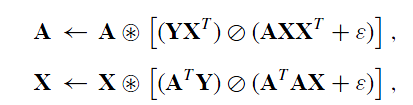
###最小二乘求解NMF###
在最小二乘中目标函数的表达式为
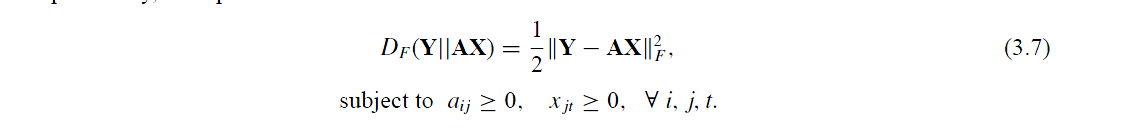然后我们对这个目标函数表达式求解KKT条件得到如下：
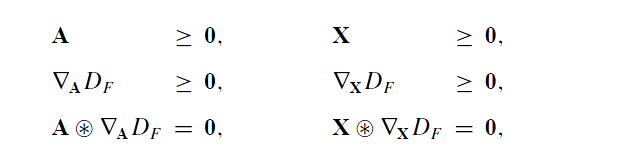求解梯度我们得到：
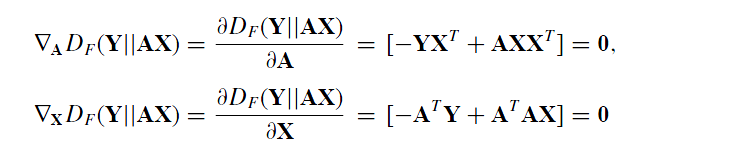
即更新的规则为:
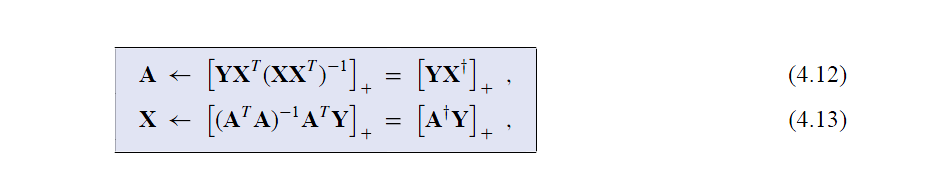
###非负矩阵收敛证明###
####定义辅助函数####
定义1：如果一个矩阵$G\left( {x,x’} \right)$，它满足以下两个条件
- \[G\left( {x,x’} \right) \ge F\left( h \right)\]
- \[G\left( {x,x} \right) = F\left( x \right)\]
我们定义函数$G\left( {x,x’} \right)$为函数 $F \left( x \right)$的辅助函数。这个函数的意思是函数G是函数F的一个上限函数。它的图示如下图所示。
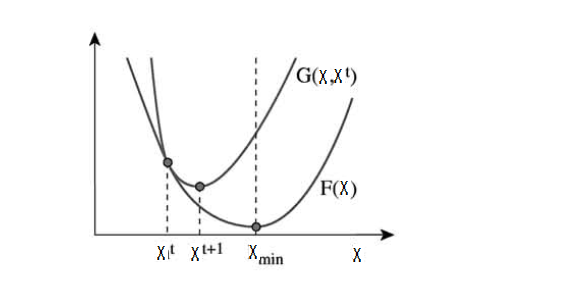
从图中我们可以发现，我们在最小化函数G即
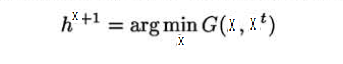
的时候，函数F是非增的。这个是因为： \[F\left( {{x^{t + 1}}} \right) \le G\left( {{x^{t + 1}},{x^t}} \right) \le G\left( {{x^t},{x^t}} \right) = F\left( {{x^t}} \right)\]
注意到当上面这个式子取等号的时候，即
\[F\left( {{x^{t + 1}}} \right) = G\left( {{x^{t + 1}},{x^t}} \right) = G\left( {{x^t},{x^t}} \right) = F\left( {{x^t}} \right)\]
这意味着点${{x^t}}$是函数$G\left( {{x^{t + 1}},{x^t}} \right)$和函数$F\left( {{x^t}} \right)$，在同一个点取得局部最优。我们通过对函数F在点${{x^t}}$的邻域进行求导可以得出 $\nabla F\left( {{x^t}} \right) = 0$
####构造辅助函数#### 下面我们根据上面的性质对目标函数\[\left|| {Y - AX} \right||\]构造辅助函数G。 函数$F\left( x \right) = \frac{1}{2}\sum \limits_i {{{\left( {{y_i} - \sum\limits_a {{A_{ia}}{x_a}} } \right)}^2}}$的辅助函数$G\left( {{x},{x^t}} \right)$定义为：
\[G\left( {x,{x^t}} \right) = F\left( {{x^t}} \right) + {\left( {x - {x^t}} \right)^T}\nabla F\left( {{x^t}} \right) + \frac{1}{2}{\left( {x - {x^t}} \right)^T}K\left( {{x^t}} \right)\left( {x - {x^t}} \right)\]
其中$K\left( {{x^t}} \right)$为一个对角矩阵。它的每一个元素定义为：
\[{K_{ab}}\left( \right) = {\delta_{ab}}{\left( {{A^T}A{x^t}} \right)_a}/x_a^t\]
我们根据辅助函数的两条性质对函数$G\left( {x,{x^t}} \right)$进行证明。
显然$G\left( {x,x} \right) = F\left( x \right)$因此我们只需证明$G\left( {x,{x^t}} \right) \ge F\left( x \right)$ 我们对函数$F\left( x \right)$进行泰勒展开得到： \[F\left( x \right) = F\left( {{x^t}} \right) + {\left( {x - {x^t}} \right)^T}\nabla F\left( \right) + \frac{1}{2}{\left( {x - {x^t}} \right)^T}{A^T}A\left( {x - {x^t}} \right)\] 如果$G\left( {x,{x^t}} \right) \ge F\left( x \right)$那么 \[{\left( {x - {x^t}} \right)^T}\left( {K\left( {{x^t}} \right){\rm{ - }}{A^T}A} \right)\left( {x - {x^t}} \right) \ge {\rm{0}}\]
即矩阵${K\left( {{x^t}} \right){\rm{ - }}{A^T}A}$半正定。即对于向量$x$我们得到：
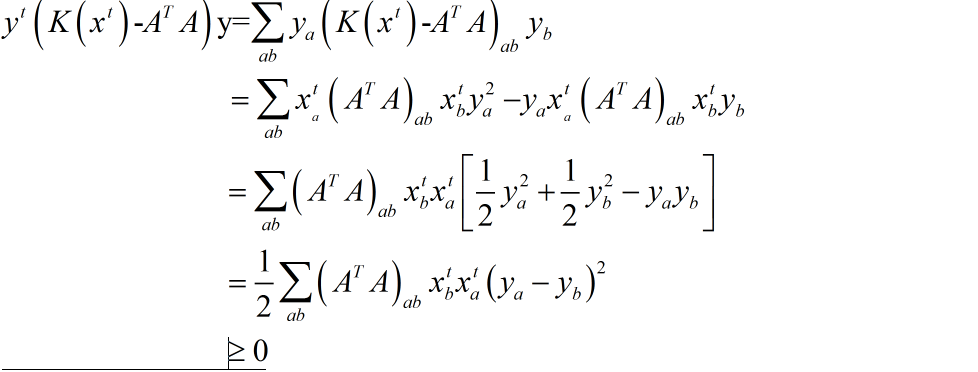
即目标函数收敛。