句法模式识别(1)-句法模式识别介绍
最近看到了一类应该来说现在很少用的模式识别方法了-句法模式识别。现在很多的模式识别方法都是统计模式识别，比如说我们常见的SVM，neural network，以及logistics regression等等。统计模式识别一般情况下都是先提取特征，然后丢到一个SVM或者Adabost等分类器中去做分类工作。而句法模式识别通常情况下用模式的基本组成元素（基元）及其相互间的结构关系对模式进行描述和识别。比如说我们要识别一个物体是否是一个矩形，统计模式识别我们可能会对这个矩形提取轮廓特征，然后进行训练一个分类器，之后再进行识别。
而在句法模式识别中，我们可以对一个矩形进行分解，它是由长和宽构成的，其中长和宽分别有两个方向具体图示如下图所示
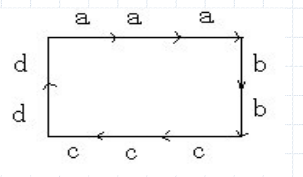如图，一个矩形由一个从左到右的长a，一个从上到下的宽b，一个从右到左的长c，一个从下到上的d构成的。而且他们的顺序是a->b->c->d，这样我们在识别矩形的时候就看一个物体是否能够表达成a-b->c->d的序列形式即可。在句法中称a,b,c,d为基元。而a->b->c->d表示基元之间的结构关系。句法模式识别利用形式语言和自动机理论给出模式类中结构关系的模型和描述。这句话提到了句法识别中的两个个关键部分一个是形式语言，一个是自动机理论。下面我们将一一进行介绍。
##字母表##
| 字母表$V$是一个有穷的符号集，句子$x$ 是由$V$中的符号形成的有穷长度的串, $x$的长度记作 ，表示$\left | x \right | $表达式中符号的数目。空串记作 $\lambda$，是一个不包含任何符号的串，它的长度为0 。字母表在我们的日常生活中很常见比如说在英语中字母表就代表26个英文字母。 |
对于任何字母表$V$ 来说，所有由 $V$中字母组成的句子的可数无穷集合(包括空串$\lambda$ )是闭包，记作 ${V^*}$ 。 $V$的正闭包${V^+}$ 可以表示成
\[{V^+}={V^*}-\left\{\lambda \right\}\]
例如，对于给定的字母表$V = \left\{ {a,c} \right\}$，它的闭包和正闭包分别是
\[\begin{array}{l}
{V^*} = \left\{ {\lambda ,a,c,aa,ac, \cdots } \right\}\
{V^ + } = \left\{ {a,c,aa,ac, \cdots } \right\}
\end{array}\]
语言表示句子的集合，即字母表中所有字母组成的一个语言${V^*}$是一个有穷子集或一个可数无穷子集。比如说英语的单词就是由26个基本字母表示而成的。
##形式语言##
形式语言领域研究的基本系统可定义为：系统给出一个规则的有穷集合，这个规则集合只用来产生属于某一特殊语言的串集合。这些句法都包括在一个文法中，这个文法可以形式地定义为一个四元组$G$
\[G = (N,\sum ,R,S)\]
其中，N表示非终结符或变量的有穷集合；$\sum$表示终结符或常数的有穷集合；$R$表示产生式或重写规则的有穷集合；$S$表示$N$中的起始符。$N \cap \sum = \Phi$ ，即为空集。文法的字母表$V$ 是$N \cup \sum $集合 。产生式的集合$R$由形式为$\alpha \to \beta $的重写规则组成，其中$\alpha$ 在${V^*}N{V^*}$， $\beta$在 ${V^*}$中。规则 $\alpha \to \beta$可理解为串 $\alpha$可以用串$\beta$ 来代替，其中 $\alpha$ 必须至少包含一个非终结符。
说了这么多，我们来举个例子，比如说下面这个
这个是一个自然语言处理的例子，根据这个形式化的语言系统我们可以很容易地通过下面的过程来构造the man sleeps 的句子。
形式语言理论可以追溯到五十年代中期乔姆斯基关于文法数学模型的研究。按照乔姆斯基的定义，文法可以分为正则文法、上下文无关文法、上下文有关文法和无约束文法四种类型。需要说明的是，句法模式识别的基本途径是把模式分解成子模式或基元。如果把每个基元解释为某种文法承认的符号，文法则是一个能生成由给定符号组成句子的句法规则的集合，根据文法规则，我们可以对。
##自动机##
自动机是有限状态机(FSM)的数学模型。FSM 是给定符号输入，依据(可表达为一个表格的)转移函数“跳转”过一系列状态的一种机器。包括：确定有限自动机DFA（扩展：下推自动机(PDA) ；线性有界自动机(LBA)；图灵机 (Turing Machine)），非确定有限自动机NFA。自动机在我们生活中也非常常见，比如说对于我们常见的贩卖机我们可以构造下面的一个自动机
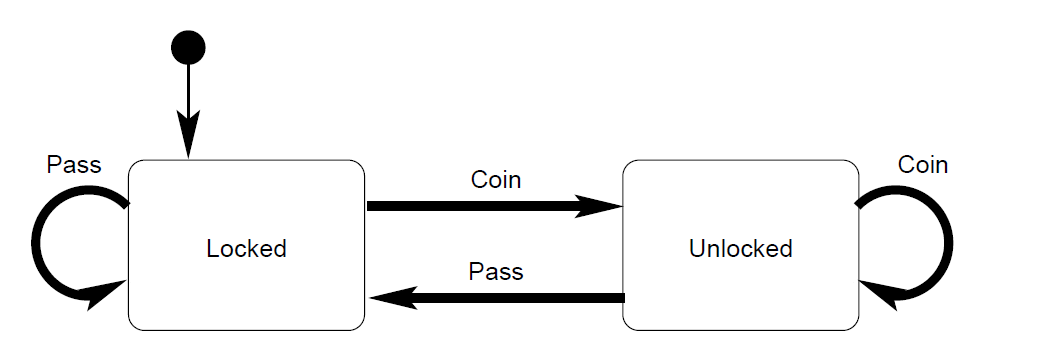
如图开始贩卖机处于关闭状态，用户没法去取饮料，用户在闸门上投入硬币或者纸币，达到一定的金额，闸门就处于解锁的状态，这样用户就可以选择饮料了。用户选择完饮料贩卖机就处于locked的状态了。从有限状态自动机的角度来考虑这个问题，那么它有两个状态即锁定状态和解锁的状态。通过投入硬币和推动旋转臂我们可以改变这两个状态。在锁定状态，无论我们如何推动旋转臂其都不会变为解锁状态。如果我们投入硬币，这样闸门就可以由锁定状态转换成解锁状态了。
自动机常常用作序列检测器即对于输入的序列，输出其是accept还是reject，我们称这种自动机为接受器和识别器（也叫做序列检测器）。它产生一个二元输出，说要么“是”要么“否”来回答输入是否被机器接受。所有自动机的状态被称为要么接受要么不接受。在所有输入都被处理了的时候，如果当前状态是接受状态，输入被接受，否则被拒绝。作为规则，输入是符号（字符）；动作不使用。下图中的例子展示了接受单词”nice”的有限状态自动机，在这个FSM中唯一的接受状态是状态7。
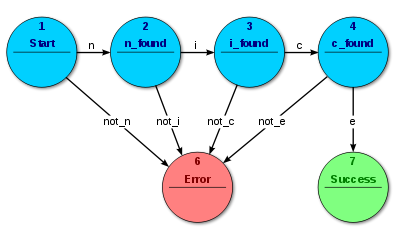
从自动机用做接收器角度来讲我们可以把形式化的语言和自动机进行对应.正则文法对应有限自动机（DAF或NFA），上下文无关文法（CFG, Context Free Grammar）对应下推自动机（有限自动机的扩展）。有限自动机只对终结符做状态转移，而下推机，可以对非终结符做状态转移。